
Материалы ОП
Как подступиться к такой сложной задаче, как понимание того, как создать интерпретатор или компилятор? В начале все это выглядит как запутанный клубок ниток, который нужно распутать, чтобы получить идеальный шар.
Чтобы достичь этого, нужно просто распутывать его по одной нитке, по одному узелку за раз. Иногда, однако, может показаться, что вы не понимаете что-то сразу, но нужно продолжать. В конце концов, все “щелкнет”, если вы будете достаточно настойчивы, я вам обещаю (Эх, если бы я откладывал по 25 центов каждый раз, когда я что-то не понимал сразу, я бы давно стал богатым :).
Вероятно, один из лучших советов, который я могу дать вам на пути к пониманию того, как создать интерпретатор и компилятор, - это читать объяснения в статьях, читать код, а затем писать код самостоятельно, и даже писать один и тот же код несколько раз в течение определенного периода времени, чтобы материал и код стали для вас естественными, и только потом переходить к изучению новых тем. Не торопитесь, просто замедлитесь и не спешите, чтобы глубоко понять основные идеи. Этот подход, хотя и кажется медленным, окупится в будущем. Поверьте мне.
В конце концов, вы получите свой идеальный клубок ниток. И знаете что? Даже если он не будет таким уж идеальным, он все равно лучше, чем альтернатива, которая заключается в том, чтобы ничего не делать и не изучать тему, или быстро пробежаться по ней и забыть через пару дней.
Помните - просто продолжайте распутывать: по одной нитке, по одному узелку за раз и практикуйте то, что вы узнали, написав код, много кода:
Сегодня вы будете использовать все знания, которые вы получили из предыдущих статей серии, и научитесь разбирать и интерпретировать арифметические выражения, содержащие любое количество операторов сложения, вычитания, умножения и деления. Вы напишете интерпретатор, который сможет вычислять выражения типа “14 + 2 * 3 - 6 / 2”.
Прежде чем погрузиться в написание кода, давайте поговорим об ассоциативности и приоритете операторов.
По соглашению 7 + 3 + 1 то же самое, что (7 + 3) + 1, а 7 - 3 - 1 эквивалентно (7 - 3) - 1. Здесь нет ничего удивительного. Мы все это выучили в какой-то момент и с тех пор принимаем это как должное. Если бы мы рассматривали 7 - 3 - 1 как 7 - (3 - 1), то результат был бы неожиданным 5 вместо ожидаемого 3.
В обычной арифметике и большинстве языков программирования сложение, вычитание, умножение и деление являются левоассоциативными:
7 + 3 + 1 эквивалентно (7 + 3) + 1 7 - 3 - 1 эквивалентно (7 - 3) - 1 8 * 4 * 2 эквивалентно (8 * 4) * 2 8 / 4 / 2 эквивалентно (8 / 4) / 2 Что означает для оператора быть левоассоциативным?
Когда операнд, такой как 3 в выражении 7 + 3 + 1, имеет знаки плюс с обеих сторон, нам нужно соглашение, чтобы решить, какой оператор применяется к 3. Тот, что слева, или тот, что справа от операнда 3? Оператор + ассоциируется слева, потому что операнд, у которого есть знаки плюс с обеих сторон, принадлежит оператору слева от него, и поэтому мы говорим, что оператор + является левоассоциативным. Вот почему 7 + 3 + 1 эквивалентно (7 + 3) + 1 по соглашению об ассоциативности.
Хорошо, а как насчет выражения типа 7 + 5 * 2, где у нас разные виды операторов с обеих сторон операнда 5? Эквивалентно ли выражение 7 + (5 * 2) или (7 + 5) * 2? Как нам разрешить эту неоднозначность?
В этом случае соглашение об ассоциативности нам не поможет, потому что оно применяется только к операторам одного вида, либо аддитивным (+, -), либо мультипликативным (*, /). Нам нужно другое соглашение, чтобы разрешить неоднозначность, когда у нас есть разные виды операторов в одном выражении. Нам нужно соглашение, которое определяет относительный приоритет операторов.
И вот оно: мы говорим, что если оператор * берет свои операнды раньше, чем +, то он имеет более высокий приоритет. В арифметике, которую мы знаем и используем, умножение и деление имеют более высокий приоритет, чем сложение и вычитание. В результате выражение 7 + 5 * 2 эквивалентно 7 + (5 * 2), а выражение 7 - 8 / 4 эквивалентно 7 - (8 / 4).
В случае, когда у нас есть выражение с операторами, которые имеют одинаковый приоритет, мы просто используем соглашение об ассоциативности и выполняем операторы слева направо:
7 + 3 - 1 эквивалентно (7 + 3) - 1 8 / 4 * 2 эквивалентно (8 / 4) * 2 Надеюсь, вы не думали, что я хотел уморить вас, так много говоря об ассоциативности и приоритете операторов. Хорошая вещь в этих соглашениях заключается в том, что мы можем построить грамматику для арифметических выражений из таблицы, которая показывает ассоциативность и приоритет арифметических операторов. Затем мы можем перевести грамматику в код, следуя рекомендациям, которые я изложил в Части 4, и наш интерпретатор сможет обрабатывать приоритет операторов в дополнение к ассоциативности.
Итак, вот наша таблица приоритетов:
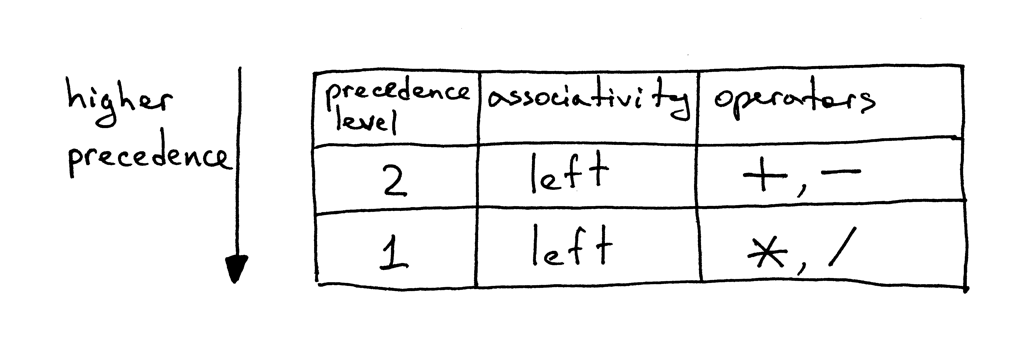
Из таблицы вы можете сказать, что операторы + и - имеют одинаковый уровень приоритета и оба являются левоассоциативными. Вы также можете видеть, что операторы * и / также являются левоассоциативными, имеют одинаковый приоритет между собой, но имеют более высокий приоритет, чем операторы сложения и вычитания.
Вот правила построения грамматики из таблицы приоритетов:
Для каждого уровня приоритета определите нетерминал. Тело продукции для нетерминала должно содержать арифметические операторы с этого уровня и нетерминалы для следующего более высокого уровня приоритета. Создайте дополнительный нетерминал factor для основных единиц выражения, в нашем случае, целых чисел. Общее правило заключается в том, что если у вас есть N уровней приоритета, вам понадобится N + 1 нетерминалов в общей сложности: один нетерминал для каждого уровня плюс один нетерминал для основных единиц выражения. Вперед!
Давайте следовать правилам и построим нашу грамматику.
Согласно Правилу 1, мы определим два нетерминала: нетерминал под названием expr для уровня 2 и нетерминал под названием term для уровня 1. И, следуя Правилу 2, мы определим нетерминал factor для основных единиц арифметических выражений, целых чисел.
Начальным символом нашей новой грамматики будет expr, и продукция expr будет содержать тело, представляющее использование операторов с уровня 2, которыми в нашем случае являются операторы + и -, и будет содержать нетерминалы term для следующего более высокого уровня приоритета, уровня 1:

Продукция term будет иметь тело, представляющее использование операторов с уровня 1, которыми являются операторы * и /, и будет содержать нетерминал factor для основных единиц выражения, целых чисел:
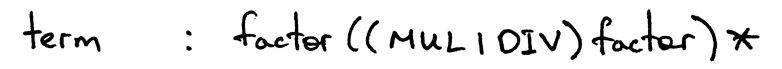
И продукция для нетерминала factor будет:
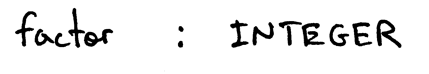
Вы уже видели вышеуказанные продукции как часть грамматик и синтаксических диаграмм из предыдущих статей, но здесь мы объединяем их в одну грамматику, которая заботится об ассоциативности и приоритете операторов:

Вот синтаксическая диаграмма, которая соответствует грамматике выше:
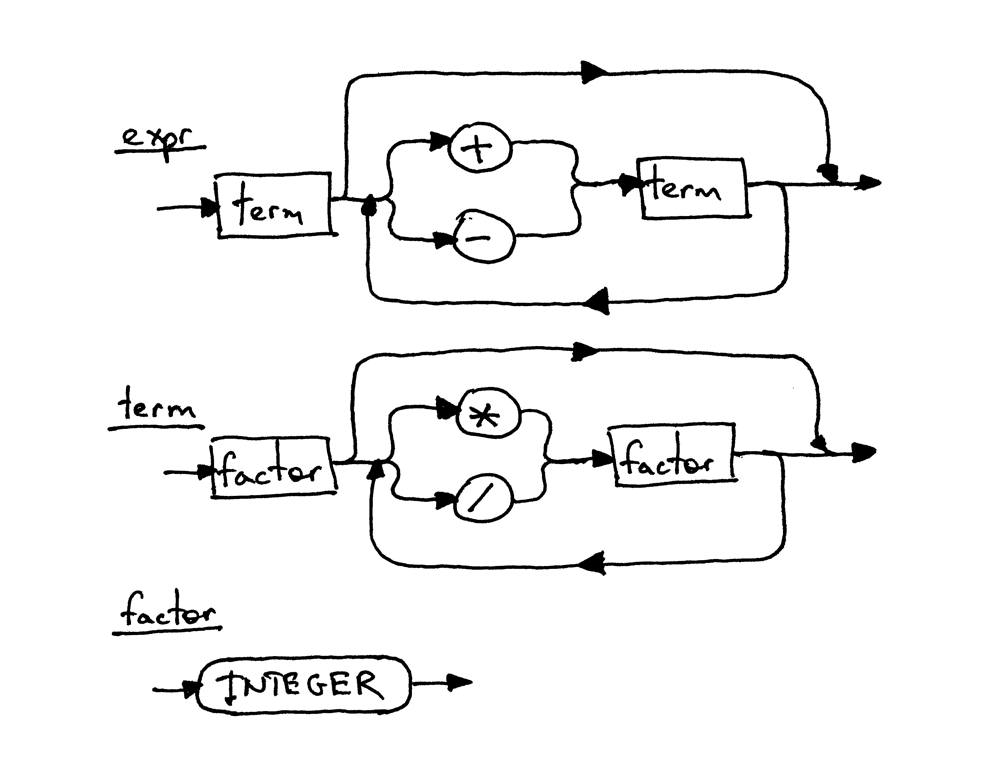
Каждый прямоугольный блок на диаграмме - это “вызов метода” к другой диаграмме. Если вы возьмете выражение 7 + 5 * 2 и начнете с верхней диаграммы expr и пройдете свой путь вниз к самой нижней диаграмме factor, вы должны увидеть, что операторы * и / с более высоким приоритетом в нижней диаграмме выполняются до операторов + и - в верхней диаграмме.
Чтобы довести до конца приоритет операторов, давайте взглянем на разложение того же арифметического выражения 7 + 5 * 2, выполненное в соответствии с нашей грамматикой и синтаксическими диаграммами выше. Это просто еще один способ показать, что операторы с более высоким приоритетом выполняются до операторов с более низким приоритетом:
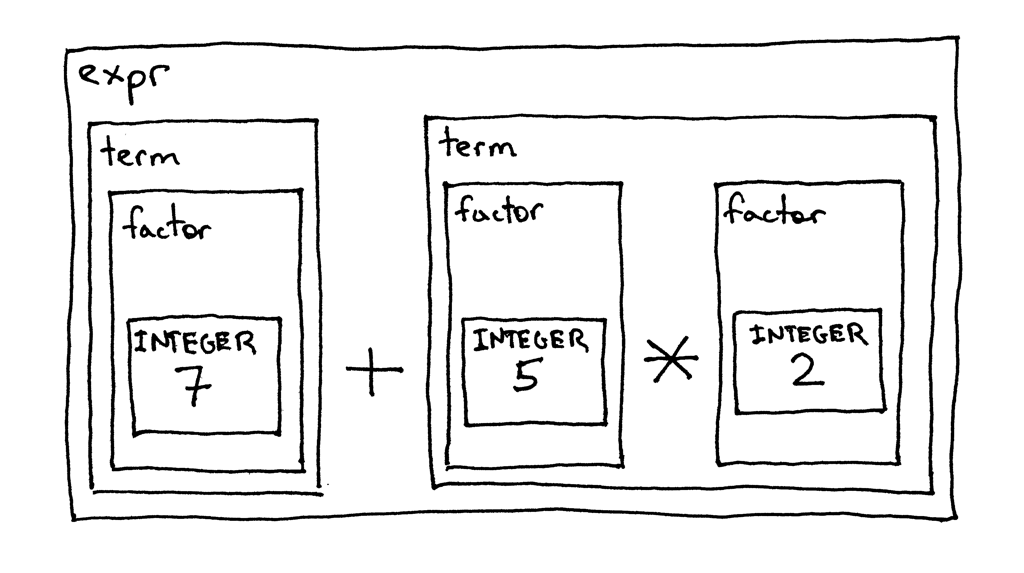
Хорошо, давайте преобразуем грамматику в код, следуя рекомендациям из Части 4, и посмотрим, как работает наш новый интерпретатор, не так ли?
Вот грамматика еще раз:

И вот полный код калькулятора, который может обрабатывать допустимые арифметические выражения, содержащие целые числа и любое количество операторов сложения, вычитания, умножения и деления.
Ниже приведены основные изменения по сравнению с кодом из Части 4:
Класс Lexer теперь может токенизировать +, -, *, и / (Здесь нет ничего нового, мы просто объединили код из предыдущих статей в один класс, который поддерживает все эти токены) Напомним, что каждое правило (продукция), R, определенное в грамматике, становится методом с тем же именем, и ссылки на это правило становятся вызовом метода: R(). В результате класс Interpreter теперь имеет три метода, которые соответствуют нетерминалам в грамматике: expr, term и factor. Исходный код:
# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, PLUS, MINUS, MUL, DIV, EOF = (
'INTEGER', 'PLUS', 'MINUS', 'MUL', 'DIV', 'EOF'
)
class Token(object):
def __init__(self, type, value):
# token type: INTEGER, PLUS, MINUS, MUL, DIV, or EOF
self.type = type
# token value: non-negative integer value, '+', '-', '*', '/', or None
self.value = value
def __str__(self):
"""String representation of the class instance.
Examples:
Token(INTEGER, 3)
Token(PLUS, '+')
Token(MUL, '*')
"""
return 'Token({type}, {value})'.format(
type=self.type,
value=repr(self.value)
)
def __repr__(self):
return self.__str__()
class Lexer(object):
def __init__(self, text):
# client string input, e.g. "3 * 5", "12 / 3 * 4", etc
self.text = text
# self.pos is an index into self.text
self.pos = 0
self.current_char = self.text[self.pos]
def error(self):
raise Exception('Invalid character')
def advance(self):
"""Advance the `pos` pointer and set the `current_char` variable."""
self.pos += 1
if self.pos > len(self.text) - 1:
self.current_char = None # Indicates end of input
else:
self.current_char = self.text[self.pos]
def skip_whitespace(self):
while self.current_char is not None and self.current_char.isspace():
self.advance()
def integer(self):
"""Return a (multidigit) integer consumed from the input."""
result = ''
while self.current_char is not None and self.current_char.isdigit():
result += self.current_char
self.advance()
return int(result)
def get_next_token(self):
"""Lexical analyzer (also known as scanner or tokenizer)
This method is responsible for breaking a sentence
apart into tokens. One token at a time.
"""
while self.current_char is not None:
if self.current_char.isspace():
self.skip_whitespace()
continue
if self.current_char.isdigit():
return Token(INTEGER, self.integer())
if self.current_char == '+':
self.advance()
return Token(PLUS, '+')
if self.current_char == '-':
self.advance()
return Token(MINUS, '-')
if self.current_char == '*':
self.advance()
return Token(MUL, '*')
if self.current_char == '/':
self.advance()
return Token(DIV, '/')
self.error()
return Token(EOF, None)
class Interpreter(object):
def __init__(self, lexer):
self.lexer = lexer
# set current token to the first token taken from the input
self.current_token = self.lexer.get_next_token()
def error(self):
raise Exception('Invalid syntax')
def eat(self, token_type):
# compare the current token type with the passed token
# type and if they match then "eat" the current token
# and assign the next token to the self.current_token,
# otherwise raise an exception.
if self.current_token.type == token_type:
self.current_token = self.lexer.get_next_token()
else:
self.error()
def factor(self):
"""factor : INTEGER"""
token = self.current_token
self.eat(INTEGER)
return token.value
def term(self):
"""term : factor ((MUL | DIV) factor)*"""
result = self.factor()
while self.current_token.type in (MUL, DIV):
token = self.current_token
if token.type == MUL:
self.eat(MUL)
result = result * self.factor()
elif token.type == DIV:
self.eat(DIV)
result = result / self.factor()
return result
def expr(self):
"""Arithmetic expression parser / interpreter.
calc> 14 + 2 * 3 - 6 / 2
17
expr : term ((PLUS | MINUS) term)*
term : factor ((MUL | DIV) factor)*
factor : INTEGER
"""
result = self.term()
while self.current_token.type in (PLUS, MINUS):
token = self.current_token
if token.type == PLUS:
self.eat(PLUS)
result = result + self.term()
elif token.type == MINUS:
self.eat(MINUS)
result = result - self.term()
return result
def main():
while True:
try:
# To run under Python3 replace 'raw_input' call
# with 'input'
text = raw_input('calc> ')
except EOFError:
break
if not text:
continue
lexer = Lexer(text)
interpreter = Interpreter(lexer)
result = interpreter.expr()
print(result)
if __name__ == '__main__':
main()
Сохраните приведенный выше код в файл calc5.py или загрузите его непосредственно с GitHub. Как обычно, попробуйте его и убедитесь сами, что интерпретатор правильно вычисляет арифметические выражения, содержащие операторы с разным приоритетом.
Вот пример сессии на моем ноутбуке:
$ python calc5.py
calc> 3
3
calc> 2 + 7 * 4
30
calc> 7 - 8 / 4
5
calc> 14 + 2 * 3 - 6 / 2
17
Вот новые упражнения на сегодня:

Напишите интерпретатор, как описано в этой статье, не заглядывая в код из статьи. Напишите несколько тестов для своего интерпретатора и убедитесь, что они проходят.
Расширьте интерпретатор для обработки арифметических выражений, содержащих круглые скобки, чтобы ваш интерпретатор мог вычислять глубоко вложенные арифметические выражения, такие как: 7 + 3 * (10 / (12 / (3 + 1) - 1))
Проверьте свое понимание.
Что означает для оператора быть левоассоциативным? Операторы + и - левоассоциативные или правоассоциативные? А как насчет * и / ? Имеет ли оператор + более высокий приоритет, чем оператор * ?
Литература
- Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
- Writing Compilers and Interpreters: A Software Engineering Approach
- Modern Compiler Implementation in Java
- Modern Compiler Design
- Compilers: Principles, Techniques, and Tools (2nd Edition)