
Материалы ОП
Как я и обещал в прошлый раз, сегодня я расскажу об одной из центральных структур данных, которую мы будем использовать на протяжении всей серии, так что пристегнитесь и поехали.
До сих пор у нас код интерпретатора и парсера был смешан, и интерпретатор вычислял выражение, как только парсер распознавал определенную языковую конструкцию, такую как сложение, вычитание, умножение или деление. Такие интерпретаторы называются синтаксически управляемыми интерпретаторами. Обычно они делают один проход по входным данным и подходят для базовых языковых приложений. Чтобы анализировать более сложные конструкции языка программирования Pascal, нам нужно построить промежуточное представление (IR). Наш парсер будет отвечать за построение IR, а наш интерпретатор будет использовать его для интерпретации входных данных, представленных в виде IR.
Оказывается, что дерево - очень подходящая структура данных для IR.
Давайте быстро поговорим о терминологии деревьев.
Дерево - это структура данных, состоящая из одного или нескольких узлов, организованных в иерархию.
У дерева есть один корень, который является верхним узлом.
Все узлы, кроме корня, имеют уникального родителя.
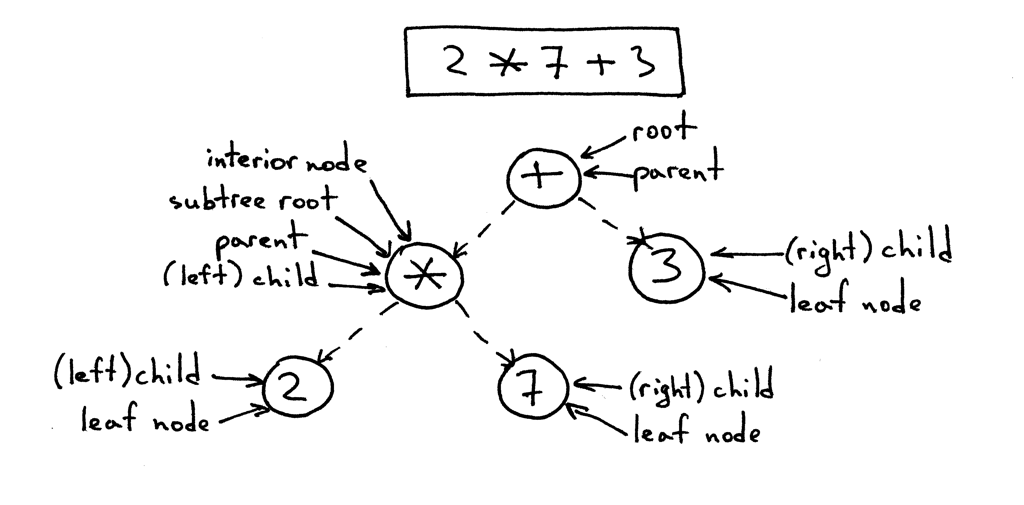
Узел, помеченный * на рисунке ниже, является родителем. Узлы, помеченные 2 и 7, являются его детьми; дети упорядочены слева направо.
Узел без потомков называется листовым узлом.
Узел, имеющий одного или нескольких потомков и не являющийся корнем, называется внутренним узлом.
Дети также могут быть полными поддеревьями. На рисунке ниже левый ребенок (помеченный *) узла + является полным поддеревом со своими детьми.
В информатике мы рисуем деревья вверх ногами, начиная с корневого узла вверху и ветвями, растущими вниз.
Вот дерево для выражения 2 * 7 + 3 с пояснениями:
IR, который мы будем использовать на протяжении всей серии, называется абстрактным синтаксическим деревом (AST). Но прежде чем мы углубимся в AST, давайте кратко поговорим о деревьях разбора. Хотя мы не собираемся использовать деревья разбора для нашего интерпретатора и компилятора, они могут помочь вам понять, как ваш парсер интерпретировал входные данные, визуализируя трассировку выполнения парсера. Мы также сравним их с AST, чтобы увидеть, почему AST лучше подходят для промежуточного представления, чем деревья разбора.
Итак, что такое дерево разбора? Дерево разбора (иногда называемое конкретным синтаксическим деревом) - это дерево, которое представляет синтаксическую структуру языковой конструкции в соответствии с нашим определением грамматики. По сути, оно показывает, как ваш парсер распознал языковую конструкцию, или, другими словами, оно показывает, как начальный символ вашей грамматики выводит определенную строку в языке программирования.
Стек вызовов парсера неявно представляет собой дерево разбора, и он автоматически строится в памяти вашим парсером, когда он пытается распознать определенную языковую конструкцию.
Давайте посмотрим на дерево разбора для выражения 2 * 7 + 3:
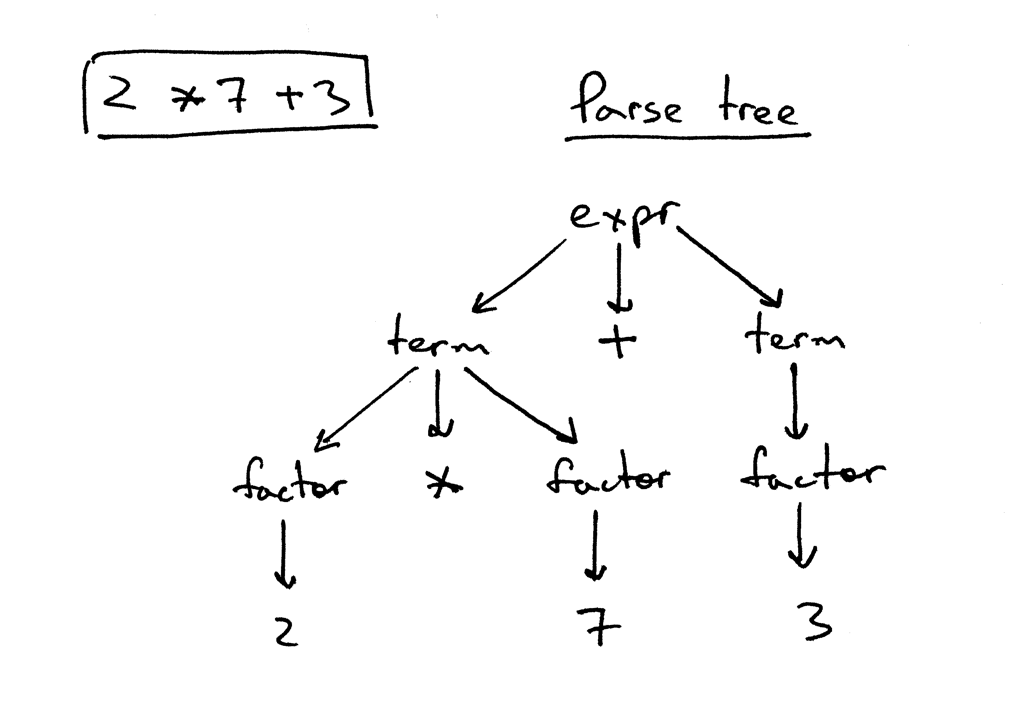
На рисунке выше вы можете видеть, что:
Дерево разбора записывает последовательность правил, которые парсер применяет для распознавания входных данных.
Корень дерева разбора помечен начальным символом грамматики.
Каждый внутренний узел представляет собой нетерминал, то есть он представляет собой применение правила грамматики, например, expr, term или factor в нашем случае.
Каждый листовой узел представляет собой токен.
Как я уже упоминал, мы не собираемся вручную строить деревья парсера и использовать их для нашего интерпретатора, но деревья разбора могут помочь вам понять, как парсер интерпретировал входные данные, визуализируя последовательность вызовов парсера.
Вы можете увидеть, как выглядят деревья разбора для различных арифметических выражений, попробовав небольшую утилиту под названием genptdot.py, которую я быстро написал, чтобы помочь вам визуализировать их. Чтобы использовать утилиту, вам сначала нужно установить пакет Graphviz, и после того, как вы выполните следующую команду, вы можете открыть сгенерированный файл изображения parsetree.png и увидеть дерево разбора для выражения, которое вы передали в качестве аргумента командной строки:
$ python genptdot.py "14 + 2 * 3 - 6 / 2" > \
parsetree.dot && dot -Tpng -o parsetree.png parsetree.dot
Вот сгенерированное изображение parsetree.png для выражения 14 + 2 * 3 - 6 / 2:
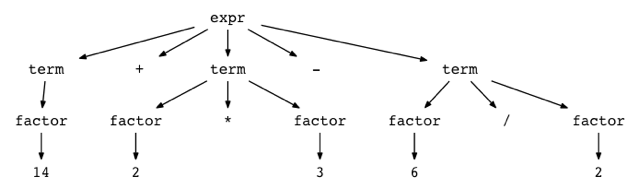
Поиграйте с утилитой, передавая ей различные арифметические выражения и посмотрите, как выглядит дерево разбора для конкретного выражения.
Теперь давайте поговорим об абстрактных синтаксических деревьях (AST). Это промежуточное представление (IR), которое мы будем активно использовать на протяжении всей серии. Это одна из центральных структур данных для нашего интерпретатора и будущих проектов компилятора.
Начнем наше обсуждение с рассмотрения как AST, так и дерева разбора для выражения 2 * 7 + 3:
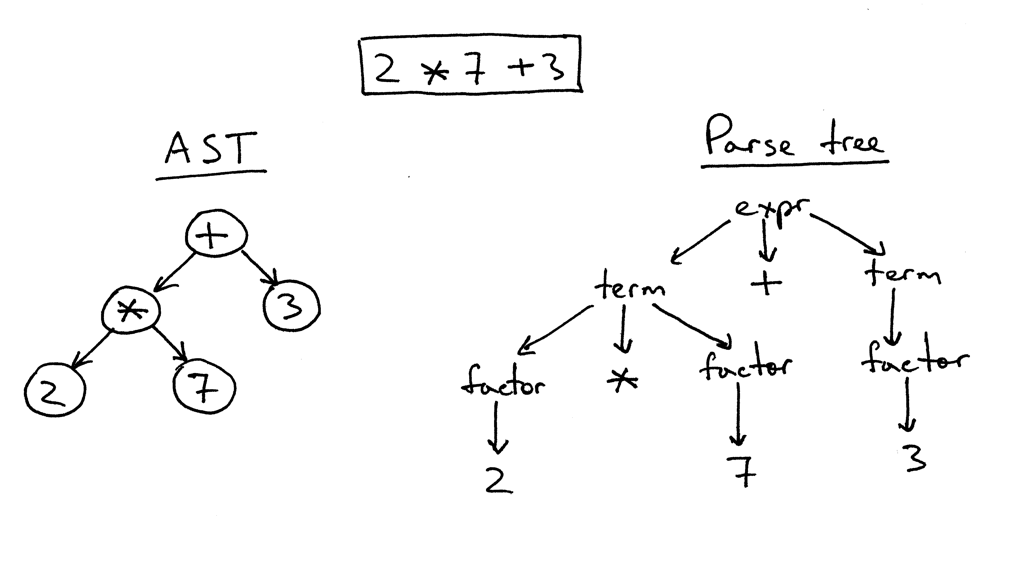
Как вы можете видеть на рисунке выше, AST захватывает суть входных данных, будучи при этом меньше.
Вот основные различия между AST и деревьями разбора:
AST использует операторы/операции в качестве корневых и внутренних узлов и использует операнды в качестве их потомков.
AST не использует внутренние узлы для представления правила грамматики, в отличие от дерева разбора.
AST не представляет каждую деталь из реального синтаксиса (поэтому они и называются абстрактными) - никаких узлов правил и никаких скобок, например.
AST плотные по сравнению с деревом разбора для той же языковой конструкции.
Итак, что такое абстрактное синтаксическое дерево? Абстрактное синтаксическое дерево (AST) - это дерево, которое представляет абстрактную синтаксическую структуру языковой конструкции, где каждый внутренний узел и корневой узел представляют собой оператор, а потомки узла представляют собой операнды этого оператора.
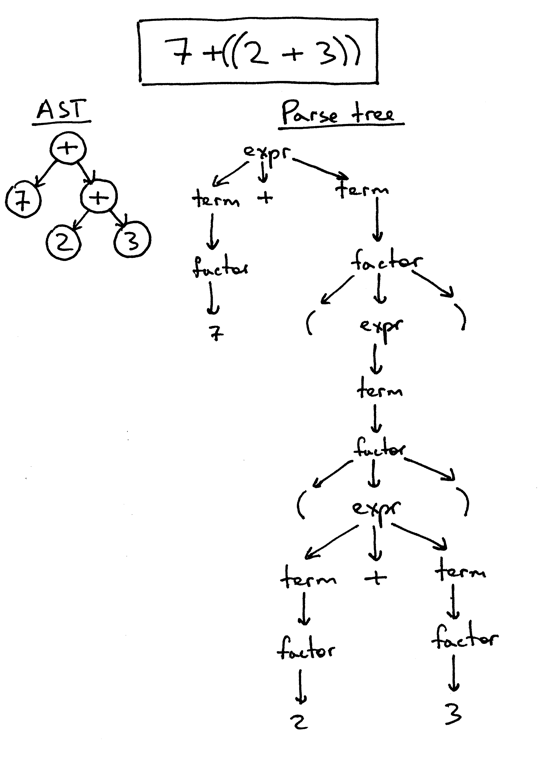
Я уже упоминал, что AST более компактны, чем деревья разбора. Давайте посмотрим на AST и дерево разбора для выражения 7 + ((2 + 3)). Вы можете видеть, что следующий AST намного меньше, чем дерево разбора, но все же захватывает суть входных данных:
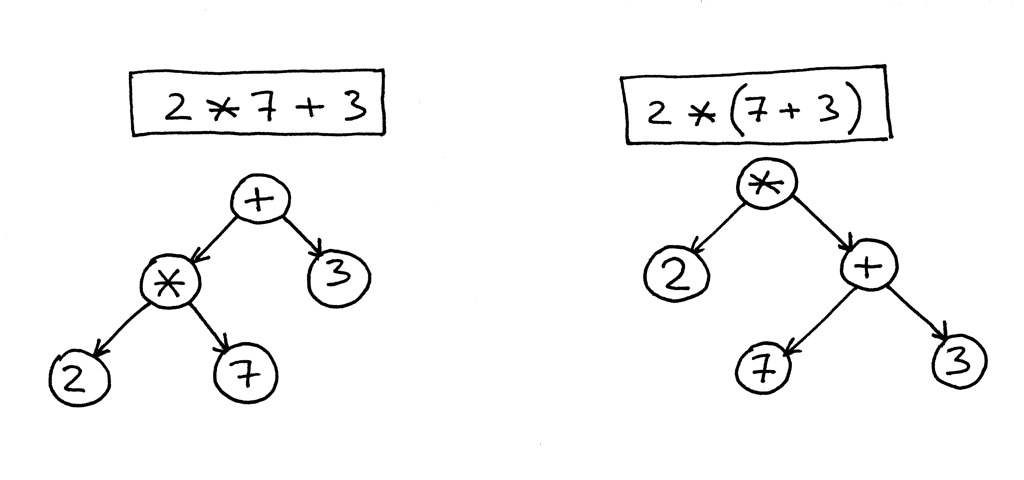
Пока все хорошо, но как закодировать приоритет операторов в AST? Чтобы закодировать приоритет операторов в AST, то есть представить, что “X происходит до Y”, вам просто нужно поместить X ниже в дереве, чем Y. И вы уже видели это на предыдущих рисунках.
Давайте посмотрим на другие примеры.
На рисунке ниже, слева, вы можете видеть AST для выражения 2 * 7 + 3. Давайте изменим приоритет, поместив 7 + 3 внутрь скобок. Вы можете видеть, справа, как выглядит AST для измененного выражения 2 * (7 + 3):
Вот AST для выражения 1 + 2 + 3 + 4 + 5:
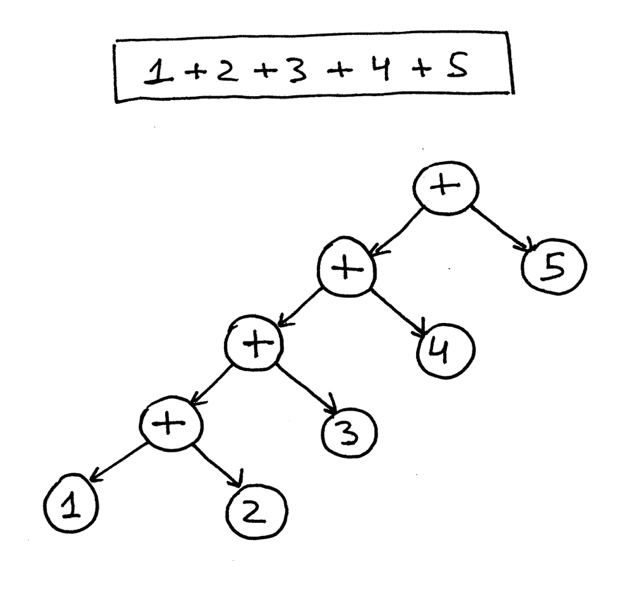
Из рисунков выше вы можете видеть, что операторы с более высоким приоритетом оказываются ниже в дереве.
Хорошо, давайте напишем немного кода для реализации различных типов узлов AST и изменим наш парсер, чтобы генерировать дерево AST, состоящее из этих узлов.
Сначала мы создадим базовый класс узла под названием AST, от которого будут наследоваться другие классы:
class AST(object):
pass
На самом деле, там не так много. Вспомните, что AST представляют модель оператор-операнд. Пока у нас есть четыре оператора и целочисленные операнды. Операторы - это сложение, вычитание, умножение и деление. Мы могли бы создать отдельный класс для представления каждого оператора, например, AddNode, SubNode, MulNode и DivNode, но вместо этого у нас будет только один класс BinOp для представления всех четырех бинарных операторов (бинарный оператор - это оператор, который оперирует двумя операндами):
class BinOp(AST):
def __init__(self, left, op, right):
self.left = left
self.token = self.op = op
self.right = right
Параметрами конструктора являются left, op и right, где left и right указывают соответственно на узел левого операнда и на узел правого операнда. Op содержит токен для самого оператора: Token(PLUS, ‘+’) для оператора сложения, Token(MINUS, ‘-’) для оператора вычитания и так далее.
Чтобы представить целые числа в нашем AST, мы определим класс Num, который будет содержать токен INTEGER и значение токена:
class Num(AST):
def __init__(self, token):
self.token = token
self.value = token.value
Как вы заметили, все узлы хранят токен, используемый для создания узла. Это в основном для удобства, и это пригодится в будущем.
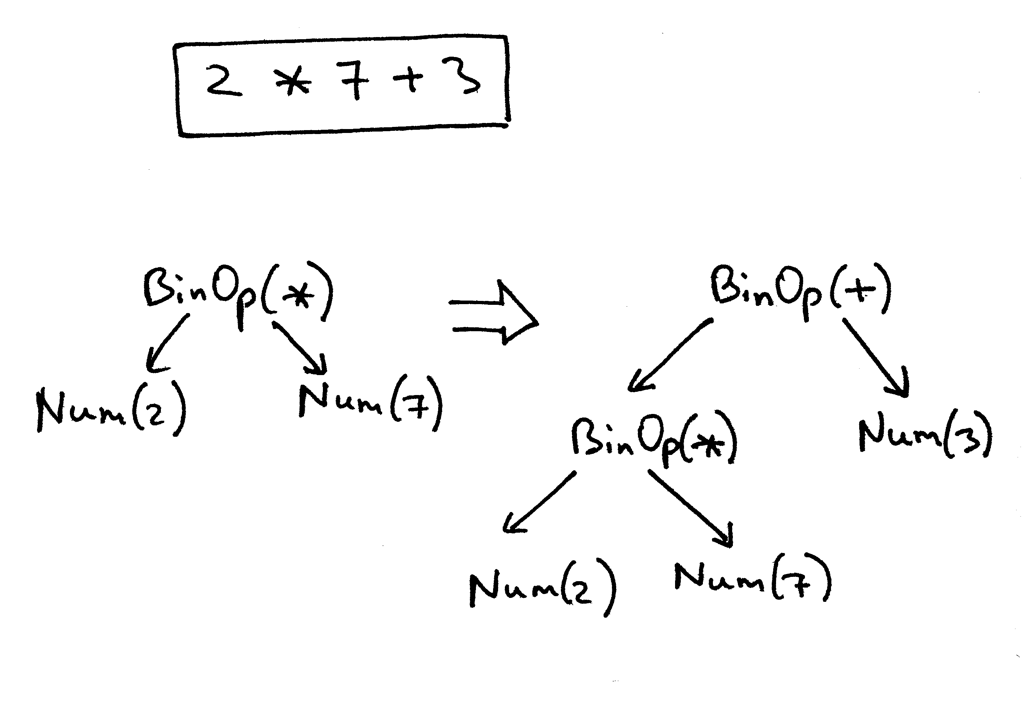
Вспомните AST для выражения 2 * 7 + 3. Мы собираемся вручную создать его в коде для этого выражения:
>>> from spi import Token, MUL, PLUS, INTEGER, Num, BinOp
>>>
>>> mul_token = Token(MUL, '*')
>>> plus_token = Token(PLUS, '+')
>>> mul_node = BinOp(
... left=Num(Token(INTEGER, 2)),
... op=mul_token,
... right=Num(Token(INTEGER, 7))
... )
>>> add_node = BinOp(
... left=mul_node,
... op=plus_token,
... right=Num(Token(INTEGER, 3))
... )
Вот как будет выглядеть AST с нашими новыми определенными классами узлов. Рисунок ниже также следует процессу ручного построения, описанному выше:
Вот наш измененный код парсера, который строит и возвращает AST в результате распознавания входных данных (арифметического выражения):
class AST(object):
pass
class BinOp(AST):
def __init__(self, left, op, right):
self.left = left
self.token = self.op = op
self.right = right
class Num(AST):
def __init__(self, token):
self.token = token
self.value = token.value
class Parser(object):
def __init__(self, lexer):
self.lexer = lexer
# set current token to the first token taken from the input
self.current_token = self.lexer.get_next_token()
def error(self):
raise Exception('Invalid syntax')
def eat(self, token_type):
# compare the current token type with the passed token
# type and if they match then "eat" the current token
# and assign the next token to the self.current_token,
# otherwise raise an exception.
if self.current_token.type == token_type:
self.current_token = self.lexer.get_next_token()
else:
self.error()
def factor(self):
"""factor : INTEGER | LPAREN expr RPAREN"""
token = self.current_token
if token.type == INTEGER:
self.eat(INTEGER)
return Num(token)
elif token.type == LPAREN:
self.eat(LPAREN)
node = self.expr()
self.eat(RPAREN)
return node
def term(self):
"""term : factor ((MUL | DIV) factor)*"""
node = self.factor()
while self.current_token.type in (MUL, DIV):
token = self.current_token
if token.type == MUL:
self.eat(MUL)
elif token.type == DIV:
self.eat(DIV)
node = BinOp(left=node, op=token, right=self.factor())
return node
def expr(self):
"""
expr : term ((PLUS | MINUS) term)*
term : factor ((MUL | DIV) factor)*
factor : INTEGER | LPAREN expr RPAREN
"""
node = self.term()
while self.current_token.type in (PLUS, MINUS):
token = self.current_token
if token.type == PLUS:
self.eat(PLUS)
elif token.type == MINUS:
self.eat(MINUS)
node = BinOp(left=node, op=token, right=self.term())
return node
def parse(self):
return self.expr()
Давайте рассмотрим процесс построения AST для некоторых арифметических выражений.
Если вы посмотрите на код парсера выше, вы увидите, что способ, которым он строит узлы AST, заключается в том, что каждый узел BinOp принимает текущее значение переменной node в качестве своего левого потомка и результат вызова term или factor в качестве своего правого потомка, поэтому он эффективно сдвигает узлы влево, и дерево для выражения 1 +2 + 3 + 4 + 5 ниже является хорошим примером этого. Вот визуальное представление того, как парсер постепенно строит AST для выражения 1 + 2 + 3 + 4 + 5:
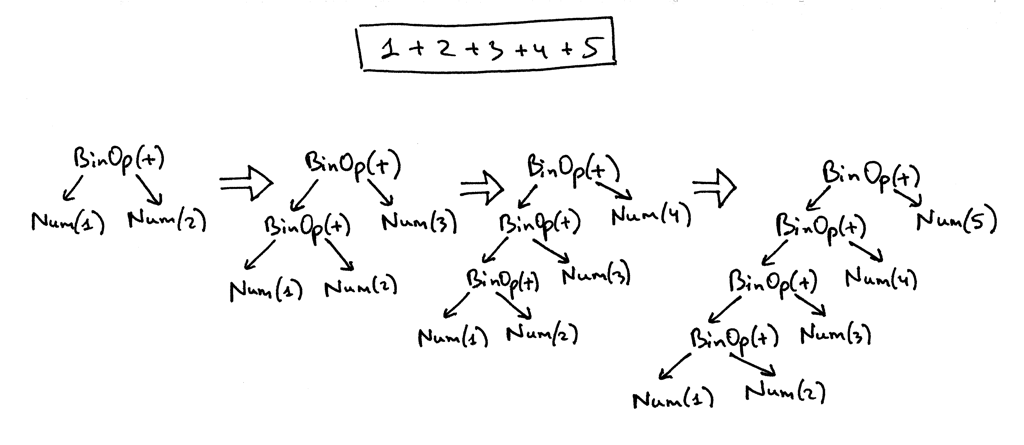
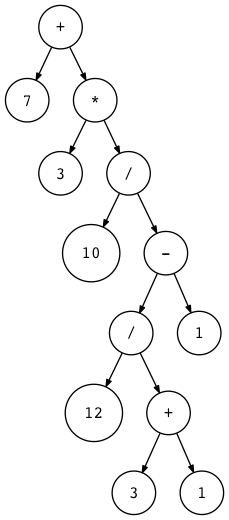
Чтобы помочь вам визуализировать AST для различных арифметических выражений, я написал небольшую утилиту, которая принимает арифметическое выражение в качестве своего первого аргумента и генерирует файл DOT, который затем обрабатывается утилитой dot для фактического рисования AST для вас (dot является частью пакета Graphviz, который вам нужно установить, чтобы запустить команду dot). Вот команда и сгенерированное изображение AST для выражения 7 + 3 * (10 / (12 / (3 + 1) - 1)):
$ python genastdot.py "7 + 3 * (10 / (12 / (3 + 1) - 1))" > \
ast.dot && dot -Tpng -o ast.png ast.dot
Стоит потратить время на то, чтобы написать несколько арифметических выражений, вручную нарисовать AST для выражений, а затем проверить их, сгенерировав изображения AST для тех же выражений с помощью инструмента genastdot.py. Это поможет вам лучше понять, как AST строятся парсером для различных арифметических выражений.
Хорошо, вот AST для выражения 2 * 7 + 3:
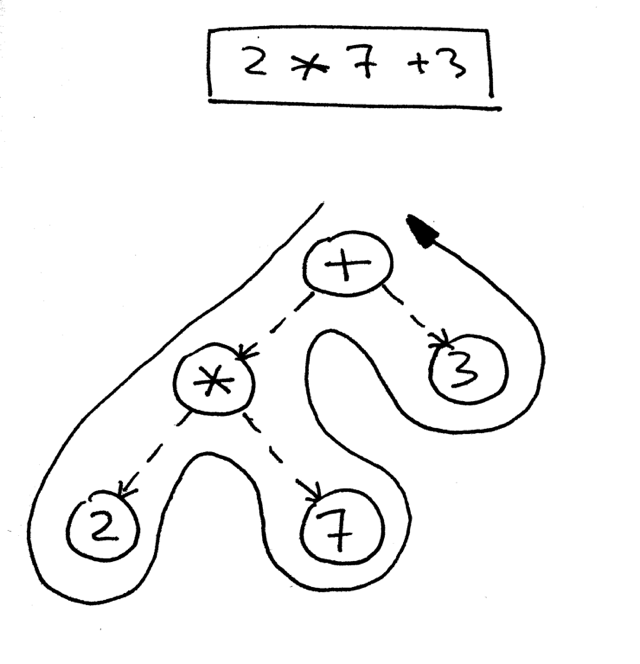
Как вы перемещаетесь по дереву, чтобы правильно вычислить выражение, представленное этим деревом? Вы делаете это с помощью обхода в постфиксной форме - частного случая обхода в глубину - который начинается с корневого узла и рекурсивно посещает потомков каждого узла слева направо. Обход в постфиксной форме посещает узлы как можно дальше от корня.
Вот псевдокод для обхода в постфиксной форме, где <<postorder actions>> - это заполнитель для действий, таких как сложение, вычитание, умножение или деление для узла BinOp, или более простого действия, такого как возврат целочисленного значения узла Num:

Причина, по которой мы собираемся использовать обход в постфиксной форме для нашего интерпретатора, заключается в том, что, во-первых, нам нужно вычислить внутренние узлы ниже в дереве, потому что они представляют операторы с более высоким приоритетом, и, во-вторых, нам нужно вычислить операнды оператора перед применением оператора к этим операндам. На рисунке ниже вы можете видеть, что при обходе в постфиксной форме мы сначала вычисляем выражение 2 * 7 и только после этого вычисляем 14 + 3, что дает нам правильный результат, 17:
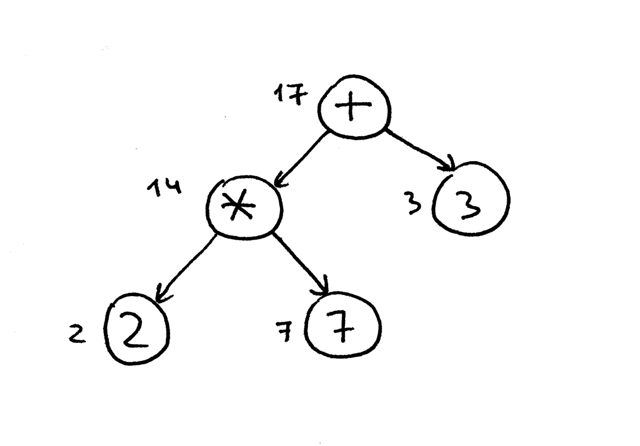
Для полноты картины я упомяну, что существует три типа обхода в глубину: обход в префиксной форме, обход в инфиксной форме и обход в постфиксной форме. Название метода обхода происходит от места, где вы помещаете действия в код посещения:

Иногда вам может потребоваться выполнить определенные действия во всех этих точках (префиксной, инфиксной и постфиксной). Вы увидите некоторые примеры этого в репозитории исходного кода для этой статьи.
Хорошо, давайте напишем немного кода для посещения и интерпретации абстрактных синтаксических деревьев, построенных нашим парсером, не так ли?
Вот исходный код, реализующий шаблон Visitor:
class NodeVisitor(object):
def visit(self, node):
method_name = 'visit_' + type(node).__name__
visitor = getattr(self, method_name, self.generic_visit)
return visitor(node)
def generic_visit(self, node):
raise Exception('No visit_{} method'.format(type(node).__name__))
А вот исходный код нашего класса Interpreter, который наследуется от класса NodeVisitor и реализует различные методы, имеющие форму visit_NodeType, где NodeType заменяется именем класса узла, таким как BinOp, Num и так далее: Есть две интересные вещи в коде, которые стоит упомянуть здесь: Во-первых, код посетителя, который манипулирует узлами AST, отделен от самих узлов AST. Вы можете видеть, что ни один из классов узлов AST (BinOp и Num) не предоставляет никакого кода для манипулирования данными, хранящимися в этих узлах. Эта логика инкапсулирована в классе Interpreter, который реализует класс NodeVisitor.
Во-вторых, вместо гигантского оператора if в методе visit класса NodeVisitor, как это:
метод visit класса NodeVisitor очень общий и отправляет вызовы соответствующему методу на основе типа узла, переданного ему. Как я уже упоминал ранее, чтобы использовать его, наш интерпретатор наследуется от класса NodeVisitor и реализует необходимые методы. Итак, если тип узла, переданного методу visit, является BinOp, то метод visit отправит вызов методу visit_BinOp, и если тип узла является Num, то метод visit отправит вызов методу visit_Num, и так далее.
Потратьте некоторое время на изучение этого подхода (стандартный модуль Python ast использует тот же механизм для обхода узлов), поскольку мы будем расширять наш интерпретатор многими новыми методами visit_NodeType в будущем.
Метод generic_visit - это резервный вариант, который вызывает исключение, чтобы указать, что он столкнулся с узлом, для которого в классе реализации нет соответствующего метода visit_NodeType.
Теперь давайте вручную построим AST для выражения 2 * 7 + 3 и передадим его нашему интерпретатору, чтобы увидеть метод visit в действии для вычисления выражения. Вот как вы можете сделать это из оболочки Python:
>>> from spi import Token, MUL, PLUS, INTEGER, Num, BinOp
>>>
>>> mul_token = Token(MUL, '*')
>>> plus_token = Token(PLUS, '+')
>>> mul_node = BinOp(
... left=Num(Token(INTEGER, 2)),
... op=mul_token,
... right=Num(Token(INTEGER, 7))
... )
>>> add_node = BinOp(
... left=mul_node,
... op=plus_token,
... right=Num(Token(INTEGER, 3))
... )
>>> from spi import Interpreter
>>> inter = Interpreter(None)
>>> inter.visit(add_node)
17
Как видите, я передал корень дерева выражения методу visit, и это вызвало обход дерева путем отправки вызовов правильным методам класса Interpreter (visit_BinOp и visit_Num) и генерации результата.
Хорошо, вот полный код нашего нового интерпретатора для вашего удобства:
""" SPI - Simple Pascal Interpreter """
###############################################################################
# #
# LEXER #
# #
###############################################################################
# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, PLUS, MINUS, MUL, DIV, LPAREN, RPAREN, EOF = (
'INTEGER', 'PLUS', 'MINUS', 'MUL', 'DIV', '(', ')', 'EOF'
)
class Token(object):
def __init__(self, type, value):
self.type = type
self.value = value
def __str__(self):
"""String representation of the class instance.
Examples:
Token(INTEGER, 3)
Token(PLUS, '+')
Token(MUL, '*')
"""
return 'Token({type}, {value})'.format(
type=self.type,
value=repr(self.value)
)
def __repr__(self):
return self.__str__()
class Lexer(object):
def __init__(self, text):
# client string input, e.g. "4 + 2 * 3 - 6 / 2"
self.text = text
# self.pos is an index into self.text
self.pos = 0
self.current_char = self.text[self.pos]
def error(self):
raise Exception('Invalid character')
def advance(self):
"""Advance the `pos` pointer and set the `current_char` variable."""
self.pos += 1
if self.pos > len(self.text) - 1:
self.current_char = None # Indicates end of input
else:
self.current_char = self.text[self.pos]
def skip_whitespace(self):
while self.current_char is not None and self.current_char.isspace():
self.advance()
def integer(self):
"""Return a (multidigit) integer consumed from the input."""
result = ''
while self.current_char is not None and self.current_char.isdigit():
result += self.current_char
self.advance()
return int(result)
def get_next_token(self):
"""Lexical analyzer (also known as scanner or tokenizer)
This method is responsible for breaking a sentence
apart into tokens. One token at a time.
"""
while self.current_char is not None:
if self.current_char.isspace():
self.skip_whitespace()
continue
if self.current_char.isdigit():
return Token(INTEGER, self.integer())
if self.current_char == '+':
self.advance()
return Token(PLUS, '+')
if self.current_char == '-':
self.advance()
return Token(MINUS, '-')
if self.current_char == '*':
self.advance()
return Token(MUL, '*')
if self.current_char == '/':
self.advance()
return Token(DIV, '/')
if self.current_char == '(':
self.advance()
return Token(LPAREN, '(')
if self.current_char == ')':
self.advance()
return Token(RPAREN, ')')
self.error()
return Token(EOF, None)
###############################################################################
# #
# PARSER #
# #
###############################################################################
class AST(object):
pass
class BinOp(AST):
def __init__(self, left, op, right):
self.left = left
self.token = self.op = op
self.right = right
class Num(AST):
def __init__(self, token):
self.token = token
self.value = token.value
class Parser(object):
def __init__(self, lexer):
self.lexer = lexer
# set current token to the first token taken from the input
self.current_token = self.lexer.get_next_token()
def error(self):
raise Exception('Invalid syntax')
def eat(self, token_type):
# compare the current token type with the passed token
# type and if they match then "eat" the current token
# and assign the next token to the self.current_token,
# otherwise raise an exception.
if self.current_token.type == token_type:
self.current_token = self.lexer.get_next_token()
else:
self.error()
def factor(self):
"""factor : INTEGER | LPAREN expr RPAREN"""
token = self.current_token
if token.type == INTEGER:
self.eat(INTEGER)
return Num(token)
elif token.type == LPAREN:
self.eat(LPAREN)
node = self.expr()
self.eat(RPAREN)
return node
def term(self):
"""term : factor ((MUL | DIV) factor)*"""
node = self.factor()
while self.current_token.type in (MUL, DIV):
token = self.current_token
if token.type == MUL:
self.eat(MUL)
elif token.type == DIV:
self.eat(DIV)
node = BinOp(left=node, op=token, right=self.factor())
return node
def expr(self):
"""
expr : term ((PLUS | MINUS) term)*
term : factor ((MUL | DIV) factor)*
factor : INTEGER | LPAREN expr RPAREN
"""
node = self.term()
while self.current_token.type in (PLUS, MINUS):
token = self.current_token
if token.type == PLUS:
self.eat(PLUS)
elif token.type == MINUS:
self.eat(MINUS)
node = BinOp(left=node, op=token, right=self.term())
return node
def parse(self):
return self.expr()
###############################################################################
# #
# INTERPRETER #
# #
###############################################################################
class NodeVisitor(object):
def visit(self, node):
method_name = 'visit_' + type(node).__name__
visitor = getattr(self, method_name, self.generic_visit)
return visitor(node)
def generic_visit(self, node):
raise Exception('No visit_{} method'.format(type(node).__name__))
class Interpreter(NodeVisitor):
def __init__(self, parser):
self.parser = parser
def visit_BinOp(self, node):
if node.op.type == PLUS:
return self.visit(node.left) + self.visit(node.right)
elif node.op.type == MINUS:
return self.visit(node.left) - self.visit(node.right)
elif node.op.type == MUL:
return self.visit(node.left) * self.visit(node.right)
elif node.op.type == DIV:
return self.visit(node.left) / self.visit(node.right)
def visit_Num(self, node):
return node.value
def interpret(self):
tree = self.parser.parse()
return self.visit(tree)
def main():
while True:
try:
try:
text = raw_input('spi> ')
except NameError: # Python3
text = input('spi> ')
except EOFError:
break
if not text:
continue
lexer = Lexer(text)
parser = Parser(lexer)
interpreter = Interpreter(parser)
result = interpreter.interpret()
print(result)
if __name__ == '__main__':
main()
Сохраните вышеуказанный код в файле spi.py или загрузите его непосредственно с GitHub. Попробуйте и посмотрите сами, что ваш новый интерпретатор на основе дерева правильно оценивает арифметические выражения.
Вот пример сеанса:
$ python spi.py
spi> 7 + 3 * (10 / (12 / (3 + 1) - 1))
22
spi> 7 + 3 * (10 / (12 / (3 + 1) - 1)) / (2 + 3) - 5 - 3 + (8)
10
spi> 7 + (((3 + 2)))
12
Сегодня вы узнали о деревьях разбора, AST, о том, как строить AST и как обходить их для интерпретации входных данных, представленных этими AST. Вы также изменили парсер и интерпретатор и разделили их.
Текущий интерфейс между лексером, парсером и интерпретатором теперь выглядит так:
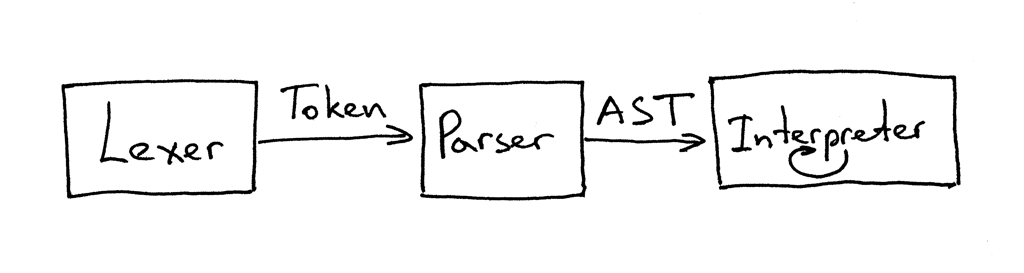
Вы можете прочитать это как “Парсер получает токены от лексера, а затем возвращает сгенерированный AST для интерпретатора для обхода и интерпретации входных данных”.
На этом на сегодня все, но прежде чем закончить, я хотел бы кратко поговорить о рекурсивных парсерах нисходящего разбора, а именно просто дать им определение, потому что я обещал в прошлый раз поговорить о них более подробно. Итак, вот оно: рекурсивный парсер нисходящего разбора - это парсер нисходящего разбора, который использует набор рекурсивных процедур для обработки входных данных. Нисходящий отражает тот факт, что парсер начинает с построения верхнего узла дерева разбора, а затем постепенно строит нижние узлы.
А теперь пришло время для упражнений :)

Напишите транслятор (подсказка: посетитель узлов), который принимает в качестве входных данных арифметическое выражение и выводит его в постфиксной нотации, также известной как обратная польская нотация (RPN). Например, если входными данными для транслятора является выражение (5 + 3) * 12 / 3, то выходными данными должно быть 5 3 + 12 * 3 /. Посмотрите ответ здесь, но попробуйте сначала решить его самостоятельно.
Напишите транслятор (посетитель узлов), который принимает в качестве входных данных арифметическое выражение и выводит его в нотации в стиле LISP, то есть 2 + 3 станет (+ 2 3), а (2 + 3 * 5) станет (+ 2 (* 3 5)). Вы можете найти ответ здесь, но опять же, попробуйте решить его сначала, прежде чем смотреть на предоставленное решение.
В следующей статье мы добавим операторы присваивания и унарные операторы в наш растущий интерпретатор Pascal. До тех пор, получайте удовольствие и до скорой встречи.
P.S. Я также предоставил реализацию интерпретатора на Rust, которую вы можете найти на GitHub. Это способ для меня изучить Rust, поэтому имейте в виду, что код может быть еще не “идиоматичным”. Комментарии и предложения о том, как улучшить код, всегда приветствуются.
Литература
- Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
- Writing Compilers and Interpreters: A Software Engineering Approach
- Modern Compiler Implementation in Java
- Modern Compiler Design
- Compilers: Principles, Techniques, and Tools (2nd Edition)