Давайте построим простой интерпретатор. Часть 8

четверг, мая 8, 2025 | 5 минут чтения

Материалы ОП

Сегодня мы поговорим об унарных операторах, а именно об унарном плюсе (+) и унарном минусе (-).

Большая часть сегодняшнего материала основана на материале из предыдущей статьи, поэтому, если вам нужно освежить знания, просто вернитесь к Части 7 и повторите ее. Помните: повторение – мать учения.

С учетом сказанного, вот что вы собираетесь сделать сегодня:

расширить грамматику для обработки унарных операторов плюс и минус
добавить новый класс узла AST UnaryOp
расширить парсер для генерации AST с узлами UnaryOp
расширить интерпретатор и добавить новый метод visit_UnaryOp для интерпретации унарных операторов

Давайте начнем, хорошо?

До сих пор мы работали только с бинарными операторами (+, -, *, /), то есть с операторами, которые оперируют двумя операндами.

Что же такое унарный оператор? Унарный оператор – это оператор, который оперирует только одним операндом.

Вот правила для унарных операторов плюс и минус:

Унарный оператор минус (-) производит отрицание своего числового операнда
Унарный оператор плюс (+) возвращает свой числовой операнд без изменений
Унарные операторы имеют более высокий приоритет, чем бинарные операторы +, -, * и /

В выражении “+ - 3” первый оператор ‘+’ представляет операцию унарного плюса, а второй оператор ‘-‘ представляет операцию унарного минуса. Выражение “+ - 3” эквивалентно “+ (- (3))”, что равно -3. Можно также сказать, что -3 в выражении является отрицательным целым числом, но в нашем случае мы рассматриваем его как унарный оператор минус с 3 в качестве его положительного целочисленного операнда:

Давайте посмотрим на другое выражение, “5 - - 2”:

В выражении “5 - - 2” первый ‘-‘ представляет операцию бинарного вычитания, а второй ‘-‘ представляет операцию унарного минуса, отрицание.

И еще несколько примеров:

Теперь давайте обновим нашу грамматику, чтобы включить унарные операторы плюс и минус. Мы изменим правило factor и добавим туда унарные операторы, потому что унарные операторы имеют более высокий приоритет, чем бинарные операторы +, -, * и /.

Вот наше текущее правило factor:

factor : INTEGER | LPAREN expr RPAREN

А вот наше обновленное правило factor для обработки унарных операторов плюс и минус:

factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN

Как видите, я расширил правило factor, чтобы оно ссылалось само на себя, что позволяет нам выводить выражения, подобные “- - - + - 3”, – допустимое выражение с большим количеством унарных операторов.

Вот полная грамматика, которая теперь может выводить выражения с унарными операторами плюс и минус:

expr   : term ((PLUS | MINUS) term)*
term   : factor ((MUL | DIV) factor)*
factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN

Следующий шаг – добавить класс узла AST для представления унарных операторов.

Вот этот подойдет:

class UnaryOp(AST):
    def __init__(self, op, expr):
        self.token = self.op = op
        self.expr = expr

Конструктор принимает два параметра: op, который представляет токен унарного оператора (плюс или минус), и expr, который представляет узел AST.

В нашей обновленной грамматике были изменения в правиле factor, поэтому именно его мы и собираемся изменить в нашем парсере – метод factor. Мы добавим код в метод для обработки подправила “(PLUS | MINUS) factor”:

def factor(self):
    """factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN"""
    token = self.current_token
    if token.type == PLUS:
        self.eat(PLUS)
        node = UnaryOp(token, self.factor())
        return node
    elif token.type == MINUS:
        self.eat(MINUS)
        node = UnaryOp(token, self.factor())
        return node
    elif token.type == INTEGER:
        self.eat(INTEGER)
        return Num(token)
    elif token.type == LPAREN:
        self.eat(LPAREN)
        node = self.expr()
        self.eat(RPAREN)
        return node

А теперь нам нужно расширить класс Interpreter и добавить метод visit_UnaryOp для интерпретации унарных узлов:

def visit_UnaryOp(self, node):
    op = node.op.type
    if op == PLUS:
        return +self.visit(node.expr)
    elif op == MINUS:
        return -self.visit(node.expr)

Вперед!

Давайте вручную построим AST для выражения “5 - - - 2” и передадим его нашему интерпретатору, чтобы убедиться, что новый метод visit_UnaryOp работает. Вот как это можно сделать из оболочки Python:

>>> from spi import BinOp, UnaryOp, Num, MINUS, INTEGER, Token
>>> five_tok = Token(INTEGER, 5)
>>> two_tok = Token(INTEGER, 2)
>>> minus_tok = Token(MINUS, '-')
>>> expr_node = BinOp(
...     Num(five_tok),
...     minus_tok,
...     UnaryOp(minus_token, UnaryOp(minus_token, Num(two_tok)))
... )
>>> from spi import Interpreter
>>> inter = Interpreter(None)
>>> inter.visit(expr_node)
3

Визуально дерево AST выше выглядит так:

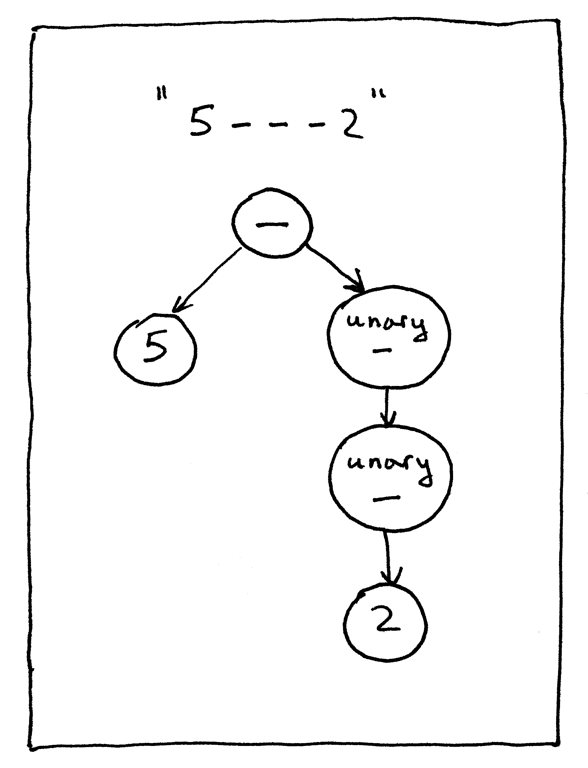
alt text

Скачайте полный исходный код интерпретатора для этой статьи прямо с GitHub. Попробуйте его и убедитесь сами, что ваш обновленный древовидный интерпретатор правильно вычисляет арифметические выражения, содержащие унарные операторы.

Вот пример сеанса:

$ python spi.py
spi> - 3
-3
spi> + 3
3
spi> 5 - - - + - 3
8
spi> 5 - - - + - (3 + 4) - +2
10

Я также обновил утилиту genastdot.py для обработки унарных операторов. Вот некоторые примеры сгенерированных изображений AST для выражений с унарными операторами:

$ python genastdot.py "- 3" > ast.dot && dot -Tpng -o ast.png ast.dot

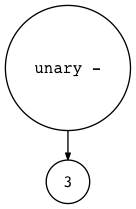
alt text

$ python genastdot.py "+ 3" > ast.dot && dot -Tpng -o ast.png ast.dot

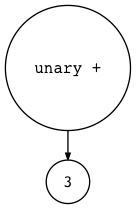
alt text

$ python genastdot.py "5 - - - + - 3" > ast.dot && dot -Tpng -o ast.png ast.dot

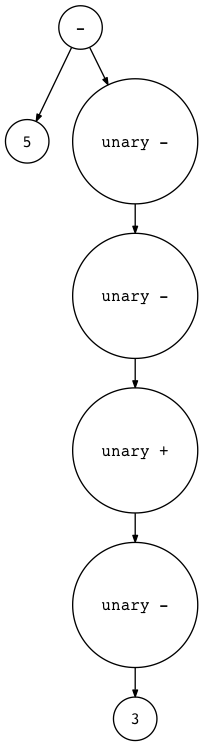
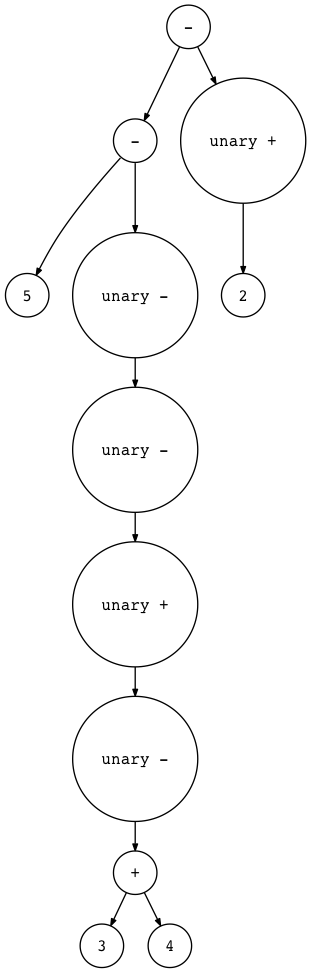
alt text

$ python genastdot.py "5 - - - + - (3 + 4) - +2" \
  > ast.dot && dot -Tpng -o ast.png ast.dot

alt text

И вот новое упражнение для вас:

alt text

Установите Free Pascal, скомпилируйте и запустите testunary.pas и убедитесь, что результаты совпадают с результатами, полученными с помощью вашего spi-интерпретатора.

Литература

Предыдущая Давайте построим простой интерпретатор. Часть 9

Следующая Давайте построим простой интерпретатор. Часть 7